مقدمه ماتریس پایه و اساس الگوریتم های معاملاتی پیچیده است زیرا به شما کمک می کند محاسبات پیچیده را بدون زحمت و بدون نیاز به توان محاسباتی زیاد انجام دهید، بدون شک ماتریس بسیاری از محاسبات را در رایانه های مدرن ممکن کرده است، زیرا همه ما می دانیم که بیت های اطلاعات هستند. به

کد خبر : 244051

تاریخ انتشار : شنبه ۲۹ مرداد ۱۴۰۱ - ۶:۲۵

کتابخانه ماتریس ها و بردارها در MQL5 – سیستم های معاملاتی – 19 اوت 2022

مقدمه

ماتریس پایه و اساس الگوریتم های معاملاتی پیچیده است زیرا به شما کمک می کند محاسبات پیچیده را بدون زحمت و بدون نیاز به توان محاسباتی زیاد انجام دهید، بدون شک ماتریس بسیاری از محاسبات را در رایانه های مدرن ممکن کرده است، زیرا همه ما می دانیم که بیت های اطلاعات هستند. به صورت آرایه ای در RAM حافظه کامپیوتر ما ذخیره می شود.

صدها یا نه هزاران عملیات ماتریسی وجود دارد، اما من برخی از مهمترین عملیات را برای دانشمندان داده و علاقه مندان به یادگیری ماشین جمع آوری کردم، همه آنها را در یک کتابخانه MQL5 کدگذاری کردم.

یک چیز خوب در مورد عملیات ماتریس این است که آنها از بیرون ساده به نظر می رسند در حالی که در داخل محاسبات زیادی را انجام می دهند که برای پایه گذاری مدل های پیچیده یادگیری ماشین مانند شبکه های عصبی مهم بوده است.

در زیر عملکرد ضروری کتابخانه و نحوه کار آنها آمده است.

کتابخانه ماتریس ها و بردارها در MQL5

این پست فرض می کند که شما درک اولیه ای از جبر خطی دارید.

خواندن یک فایل CSV به ماتریس

این غیرقابل انکار است که قبل از اینکه بتوانید هر مدلی بسازید یا هر گونه تجزیه و تحلیل داده را انجام دهید، باید مجموعه داده خود را وارد کنید و رایج ترین نوع فایلی که برای ذخیره یک مجموعه داده استفاده می شود یک فایل CSV است، برای خواندن یک فایل csv در MQL5 و ذخیره آن. در یک ماتریس این خط کد را اجرا کنید

   double Matrix[]; int rows, cols;
   
   CSVToMatrix(Matrix,rows,cols,"Apple Dataset.csv");
   MatrixPrint(Matrix,cols);

خروجی در سیاهههای مربوط،

FI      0       18:24:45.319    TestLibraryEA (#NQ100،H1)       ماتریس NN      0       18:24:45.319    TestLibraryEA (#NQ100،H1)       [ 
EL      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         1.00000   1.00000   0.05000   2.62111   1.51234   0.31000  20.80000 157.64999
FL      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         2.00000   1.00000   0.14000   2.15134   1.34945   0.31000  20.80000 174.61000
RM      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         3.00000   1.00000   0.14000   2.28617   1.15921   0.31000  20.80000 165.11999
MM      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         4.00000   1.00000   0.17000   2.20677   0.96751   0.36000  19.76000 174.78000
LN      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         5.00000   1.00000   0.20000   2.00355   0.94014   0.36000  19.76000 177.57001
KN      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         6.00000   1.00000   0.20000   1.12156   0.95020   0.36000  19.76000 165.30000
IN      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         7.00000   1.00000   0.17000   1.34078   0.95775   0.44000  17.44000 149.80000
RO      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         8.00000   1.00000   0.18000   1.15018   0.91710   0.44000  17.44000 141.50000
GO      0       18:24:45.319    TestLibraryEA (#NQ100,H1)         9.00000   1.00000   0.19000   1.11831   0.81439   0.44000  17.44000 151.83000
NN      0       18:24:45.319    TestLibraryEA (#NQ100,H1)        10.00000   1.00000   0.20000   1.16670   0.60272   0.54000  16.01000 145.86000
NQ      0       18:24:45.319    TestLibraryEA (#NQ100,H1)        11.00000   1.00000   0.20000   1.08454   0.67206   0.54000  16.01000 136.96001

Here is the difference

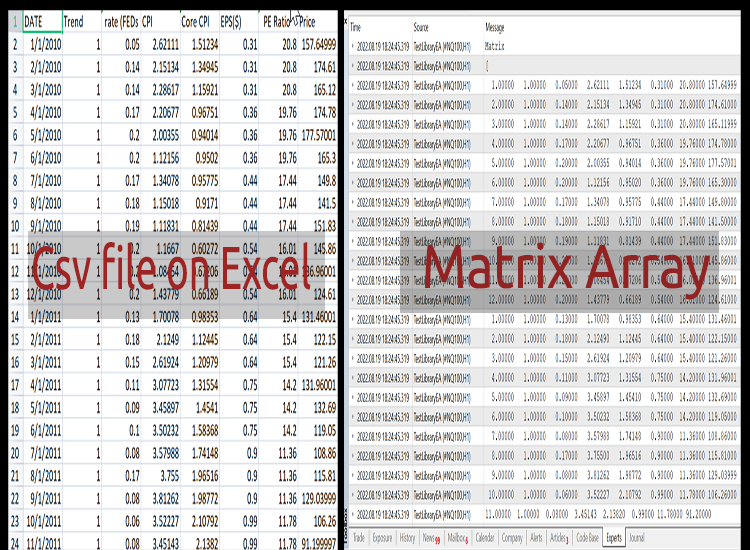
Ensure there are no strings in the csv file or date formatted values as they could be misinterpreted

Printing the Matrix

This is a very useful function in the library, It is for the sake of printing matrices, The above matrix that was obtained from a csv file has been printed using this funtion, plug in the matrix and put the number of colums available on the inside and you are good to go

   MatrixPrint(Matrix,cols);

Checking if the Matrix is a Square one

This is another useful feature, it lets you know if the matrix plugged in is a square one or not. why is this important?

To find the inverse of a matrix it has to be a square one so this function will let you make sure about that, It returns true if the matrix is a square one otherwise returns false

bool   IsMatrixSquare(double &Matrix[])

برای مثال: بیایید ببینیم که آیا ماتریس بالا مربع است یا خیر

Print("Is this matrix a square ",IsMatrixSquare(Matrix));

خروجی

DS      0       21:38:34.070    TestLibraryEA (#NQ100,H1)       Is this matrix a square false

ضرب ماتریس

این تابع به شما امکان می دهد زمانی که دو ماتریس ضرب می شوند، ماتریس نتیجه را پیدا کنید.

   double A[3] = {3,4,2}, B[12] = {13,9,7,15, 8,7,4,6 ,6,4,0,3};
   mat.MatrixMultiply(A,B,AxB,3,3,rows,cols);
   mat.MatrixPrint(AxB,cols);

مطمئن شوید که تعداد ستون‌های ماتریس اول با تعداد ردیف‌های ماتریس دوم مطابقت دارد، این قانون شماره یک ضرب ماتریس است.

در کد بالا A ماتریس 1×3 است در حالی که B ماتریس 3×4 است، ماتریس حاصل 1×4 خواهد بود.

در اینجا خروجی است.

IO      0       21:49:55.480    TestLibraryEA (#NQ100,H1)       Matrix
QD      0       21:49:55.480    TestLibraryEA (#NQ100,H1)       [ 
RS      0       21:49:55.482    TestLibraryEA (#NQ100,H1)       83.00000 63.00000 37.00000 75.00000
KD      0       21:49:55.482    TestLibraryEA (#NQ100,H1)       ] 
MS      0       21:49:55.482    TestLibraryEA (#NQ100,H1)       rows = 1 cols = 4

ماتریس Transpose و Matrix Un-transpose

هنگام ساخت شبکه عصبی، یا سایر مدل‌های یادگیری ماشین، اغلب لازم است ماتریس‌های خود را جابه‌جا و غیرقابل انتقال کنید، جابجایی ماتریس به معنای تغییر ردیف‌ها به ستون‌ها و برعکس هنگام جابجایی غیرقابل تغییر است، اجازه دهید از موارد بالا استفاده کنیم. ماتریس B

JR      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       Before transpose
EG      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       Matrix
ML      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       [ 
LK      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       13.00000  9.00000  7.00000 15.00000
MQ      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       8.00000 7.00000 4.00000 6.00000
OF      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       6.00000 4.00000 0.00000 3.00000
IQ      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       ] 
IF      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       rows = 3 cols = 4
EM      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       After transpose
KG      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       Matrix
CM      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       [ 
LI      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       13.00000  8.00000  6.00000
RS      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       9.00000 7.00000 4.00000
OH      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       7.00000 4.00000 0.00000
CS      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       15.00000  6.00000  3.00000
ED      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       ] 
ES      0       22:03:24.115    TestLibraryEA (#NQ100,H1)       rows = 4 cols = 3

در اینجا نحوه اجرای تابع Transpose آورده شده است

   double B[12] = {13,9,7,15, 8,7,4,6 ,6,4,0,3};
   
   Print("Before transpose");
   int columns = 4;
   MatrixPrint(B,columns);
   MatrixTranspose(B,columns);
   Print("After transpose");
   MatrixPrint(B,columns);

برعکسش رو ببینیم

   Print("Before Untranspose");
   int to_columns = 3;
   MatrixPrint(B,to_columns);
   MatrixTranspose(B,to_columns);
   Print("After Untranspose");
   MatrixPrint(B,to_columns);

خروجی ها،

NI      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       Before Untranspose
DO      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       Matrix
LE      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       [ 
CQ      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       13.00000  8.00000  6.00000
IK      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       9.00000 7.00000 4.00000
HP      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       7.00000 4.00000 0.00000
DJ      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       15.00000  6.00000  3.00000
FS      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       ] 
FH      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       rows = 4 cols = 3
OS      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       After Untranspose
LJ      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       Matrix
DO      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       [ 
EL      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       13.00000  9.00000  7.00000 15.00000
HR      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       8.00000 7.00000 4.00000 6.00000
RH      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       6.00000 4.00000 0.00000 3.00000
LL      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       ] 
LK      0       22:06:36.385    TestLibraryEA (#NQ100,H1)       rows = 3 cols = 4

همه چیز به همان جایی که بود بازگشته است.

ماتریس معکوس

پیدا کردن معکوس یک ماتریس مربع با استفاده از تابع نسبتاً ساده است

    void   MatrixInverse(double &Matrix[]);

برای پیدا کردن معکوس یک ماتریس 2×2 فقط

گاوس جردن معکوس

این یک روش قدرتمند برای یافتن معکوس ماتریس های بزرگتر از 2×2 است که می تواند 4×4،5×5 یا حتی 10×10 باشد.

  void   Gauss_JordanInverse(double &Matrix[],int mat_order);

double squarematrix[9] = {3,5,23, 21,7,9, 0,2,11};
      
MatrixPrint(squarematrix,3); 
      
Gauss_JordanInverse(squarematrix,3);
MatrixPrint(squarematrix,3);

خروجی

MF      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       Matrix
ES      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       [ 
CK      0       22:41:34.628    TestLibraryEA (#NQ100,H1)        3.00000  5.00000 23.00000
MR      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       21.00000  7.00000  9.00000
HE      0       22:41:34.628    TestLibraryEA (#NQ100,H1)        0.00000  2.00000 11.00000
GR      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       ] 
FI      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       rows = 3 cols = 3
RN      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       Inverse
MJ      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       Matrix
EO      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       [ 
PN      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       -4.91667  0.75000  9.66667
FE      0       22:41:34.628    TestLibraryEA (#NQ100,H1)        19.25000  -2.75000 -38.00000
CH      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       -3.50000  0.50000  7.00000
MN      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       ] 
PM      0       22:41:34.628    TestLibraryEA (#NQ100,H1)       rows = 3 cols = 3

حذف یک ستون در ماتریس

گاهی اوقات ممکن است ستون ناخواسته ای در ماتریس وجود داشته باشد که می خواهید حذف کنید

 void   MatrixRemoveColumn(double &dataArr[],int column,int rows);

حذف کل ردیف در ماتریس

این همان حذف ستون است اما رویکرد متفاوتی دارد

void   MatrixRemoveColumn(double &dataArr[],int column,int rows);

بسیاری از کارکردهای دیگر برای کاوش در کتابخانه ای وجود دارد که من در بازار به فروش می رسانم که در اینجا پیوند داده شده است https://www.mql5.com/en/market/product/81533

کد منبع پس از خرید برای توسعه و تولید سیستم های معاملاتی شما ارائه می شود.

با تشکر برای خواندن

لینک منبع : هوشمند نیوز

لینک کوتاه

برچسب ها :MQL5 ، اوت ، بردارها ، در ، سیستم ، کتابخانه ، ماتریس ، معاملاتی ، ها ، های

ارسال نظر شما

مجموع نظرات : 0 در انتظار بررسی : 0 انتشار یافته : ۰

نظرات ارسال شده توسط شما، پس از تایید توسط مدیران سایت منتشر خواهد شد.
نظراتی که حاوی تهمت یا افترا باشد منتشر نخواهد شد.
نظراتی که به غیر از زبان فارسی یا غیر مرتبط با خبر باشد منتشر نخواهد شد.

آموزش مجازی مدیریت عالی حرفه ای کسب و کار Post DBA + مدرک معتبر قابل ترجمه رسمی با مهر دادگستری و وزارت امور خارجه	آموزش مجازی مدیریت عالی و حرفه ای کسب و کار DBA + مدرک معتبر قابل ترجمه رسمی با مهر دادگستری و وزارت امور خارجه	آموزش مجازی مدیریت کسب و کار MBA + مدرک معتبر قابل ترجمه رسمی با مهر دادگستری و وزارت امور خارجه
مدیریت حرفه ای کافی شاپ	حقوقدان خبره	سرآشپز حرفه ای
آموزش مجازی تعمیرات موبایل	آموزش مجازی ICDL مهارت های رایانه کار درجه یک و دو	آموزش مجازی کارشناس معاملات املاک_ مشاور املاک