سریع و ایمن 2-از-2 ECDSA با استفاده از DKLs18

ما قبلاً در مورد مفاهیم کلی بحث کرده ایم امضای دیجیتال و امضاهای آستانه در پست قبلی در Coinbase، ما توجه خود را به طور خاص بر روی امضای آستانه دو طرفه متمرکز کرده ایم. در این پست در مورد این تنظیم بحث خواهیم کرد.

DKLs: مقدمه. در حالی که پروتکل‌های امضای آستانه برای طرح‌های Schnorr و BLS نسبتاً ساده هستند، آستانه ECDSA بسیار سخت‌تر است. تعدادی پروتکل برای امضای 2-از-2 ECDSA وجود دارد. برخی به صراحت آن را هدف قرار می دهند (یعنی از گزینه های عمومی تر پشتیبانی نمی کنند تی و n). در این پست وبلاگ صرفاً توضیحی، به طور خاص یکی را مطالعه خواهیم کرد: پروتکل 2018 Doerner، Kondi، Lee و shelat. این پروتکل بر اساس کارهای قبلی چو و اورلاندی و کلر، اورسینی و شول است. این پروتکل – یا به اختصار “DKLs” – به دو طرف اجازه می دهد تا به طور ایمن امضای ECDSA را تنها در چند میلی ثانیه، تنها با تبادل 3 پیام، و در عین حال انتقال حدود 120 کیلوبایت کل داده، تولید کنند. در این فرآیند، از چند تکنیک جالب در محاسبات دو طرفه ایمن استفاده می‌کند و نشان‌دهنده کمک منظم و چشمگیر در این زمینه است.

بیایید اکنون چند نکته فنی در مورد نحوه عملکرد DKL ها بگوییم. ایده اصلی مربوط به به اشتراک گذاری راز ضربی عناصر میدان اول اگر دو طرف ما – مثلاً آلیس و باب – به صورت محلی اسکالرهای تصادفی تولید کنند sk_A و sk_B در 𝔽_q، سپس، پس از انجام یک مبادله دیفی-هلمن، طرفین ممکن است به طور متقابل کلید عمومی مشترک را استخراج کنند. پ = sk_A · sk_B · جی، بدون اینکه چیزی در مورد سهام کلید مربوطه یکدیگر (یا کلید مخفی مشترک) یاد بگیرید. کلید مخفی مشترک محصول است sk := sk_A · sk_B (Mod q). DKLها در استفاده از اشتراک گذاری ضربی غیرعادی هستند. پروتکل نمی تواند به (تی، n) اساساً به همین دلیل تنظیم می شود.

طرفین فرآیند ECDSA را برای امضای یک پیام خاص آغاز می کنند متر به روشی مشابه آنها سهام غیر مستقیم تولید می کنند k_A و k_B به صورت تصادفی، و R := را بسازید k_A · k_B · جی همانطور که آنها انجام دادند پ; با استفاده از مختصات R (ایکس، y، هر دو اولین مؤلفه امضا را به دست می آورند r := ایکس (Mod پ). تنها برای طرفین باقی می ماند که به طور مشترک بسازند س := اچ(متر) · ک⁻¹ + r · sk · ک⁻¹ (Mod q، همانطور که توسط تعریف ECDSA تجویز شده است. مشکل اینجاست که طرفین فقط دارند اشتراک های ضربی از مقادیر ک و skو نه خود مقادیر مورد نیاز.

DKLs مشاهده می کند که عبارت تعریف می کند س به همین خوبی می توان نوشت:

https://medium.com/media/2a0c40a041fc6a2fe623305df1fa751c/href

اولین ایده کلیدی این است که آن را خواهد بود به اندازه کافی برای طرفین برای به دست آوردن اشتراکات افزودنی تصادفی دو عبارت محصول 1/k_A · 1/k_B و sk_A / k_A · sk_B / k_B در بالا. در واقع، اگر قرار بود طرفین چنین سهامی را به دست آورند، هر دو می توانند با ضرب این سهام محلی در اچ(متر) و r، به ترتیب، و افزودن نتایج (به یاد داشته باشید که هر دو طرف می دانند اچ(متر) و r). با انجام این کار، طرفین به اشتراک گذاری افزودنی از س خود، که در نهایت می توانند با خیال راحت مبادله کنند (یعنی بدون درز اطلاعات بیشتر در مورد). سجمع های فردی). در نهایت توجه داشته باشید که آلیس می تواند ضربدر سمت چپ را به صورت محلی محاسبه کند 1/k_A و sk_A/k_A; باب نیز می تواند به صورت محلی ضرب های سمت راست را محاسبه کند 1/k_B و sk_B/k_B.

بنابراین برای حل مشکل «ضرب امن» که گاهی اوقات «تبدیل ضرب به جمع» نامیده می شود، کافی است. در این مشکل، دو طرف اسکالرهای ورودی مربوطه را ارسال می کنند i_A و i_A، و با تصادفی تمام می شود افزودنی سهام t_a و t_b از محصول i_A · i_B (Mod q). به عبارت دیگر هویت t_A + t_B = i_A · i_B (Mod q) باید نگه داشته شود، و علاوه بر آن خروجی ها t_A و t_B باید به صورت تصادفی مشمول این شرط باشد. در نهایت، طرفین نباید چیزی در مورد ورودی های یکدیگر یاد بگیرند i_A و i_B در فرآیند اجرای پروتکل (حتی اگر آنها درگیر رفتارهای مخرب باشند).

DKLs یک زیرپروتکل ضرب ایمن جذاب را با استفاده از یک پروتکل اولیه دیگر به نام توصیف می کند انتقال فراموشی مرتبط (به اختصار cOT). در یک پروتکل coT، طرفین آلیس و باب نقش های نامتقارن دارند. آلیس یک اسکالر واحد، مثلاً ɑ، را در 𝔽_ وارد می کندq; Bob فقط یک بیت را وارد می کند ب. طرفین هر کدام یک اسکالر به عنوان خروجی دریافت می کنند. بیایید دوباره اینها را صدا کنیم t_A و t_B در حال حاضر با تعریف cOT، خروجی ها t_A و t_B باید به صورت تصادفی مشروط به این شرط باشد که t_A + t_B = ɑ اگر بیت ورودی باب ب 1 است و موضوع تصادفی است t_A + t_B = 0 اگر بیت ورودی باب 0 است. در هر صورت، فرستنده نباید چیزی در مورد بیت گیرنده یاد بگیرد. ب، و گیرنده نباید چیزی در مورد اسکالر ɑ فرستنده یاد بگیرد. تعریف انتقال فراموشی همبسته در شکل زیر نشان داده شده است.

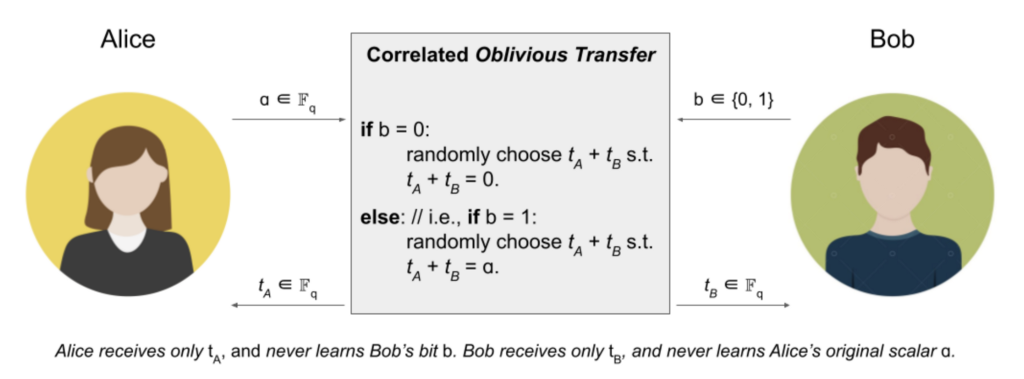
با فرض اینکه یک پروتکل cOT در دست داریم، چگونه می توانیم آن را در یک پروتکل ضربی بوت کنیم؟ جالب اینجاست که آلیس و باب می توانند از یک الگوریتم دوران ابتدایی برای این کار استفاده کنند. بیایید به اصطلاح به یاد بیاوریم ضرب طولانی الگوریتم تقریباً، این رویه به طور متوالی ضریب بالایی را هر بار یک مکان به سمت چپ تغییر می دهد. در هر مرحله نیز این ضریب را در رقم مناسب ضریب پایین ضرب می کند. در نهایت، آرایه حاصل از اعداد جابجا شده و ضرب شده را اضافه می کند. در باینری، همه چیز حتی ساده‌تر می‌شود، زیرا «ارقام» ضرب‌کننده پایین هر کدام 0 یا 1 هستند. شکلی که این فرآیند را نشان می‌دهد در زیر نشان داده شده است:

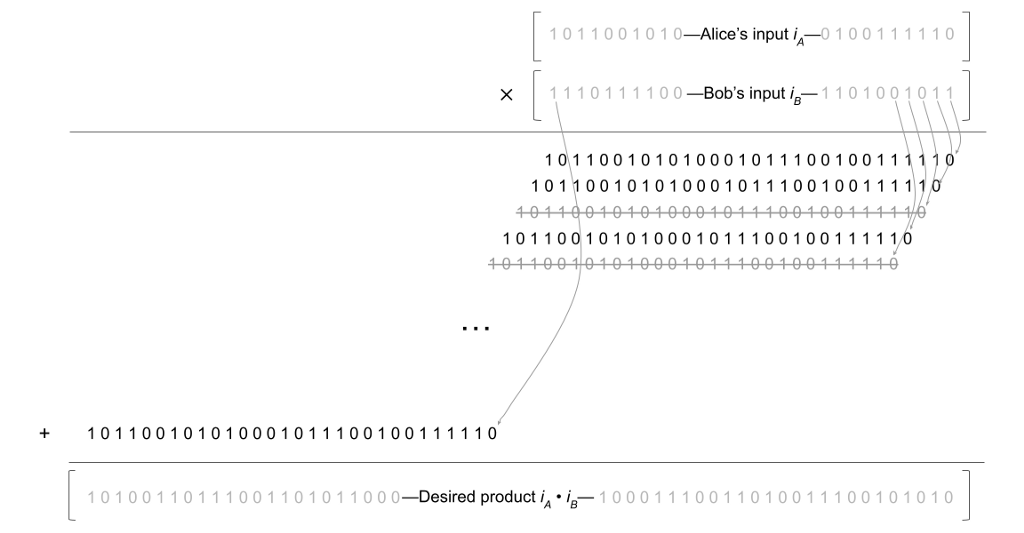
در هر ردیف از این شکل، ورودی اصلی آلیس یک مرحله بیشتر به سمت چپ منتقل می شود. علاوه بر این، با کار کردن از راست به چپ از طریق ورودی Bob، ما همچنین ردیف‌های مربوط به بیت‌هایی را که ورودی باب 0 است، حذف می‌کنیم. در نهایت، اعداد حاصل را جمع می‌کنیم تا محصول را بدست آوریم. (در واقعیت، همه چیز در اینجا اتفاق می افتد q، اما برای وضوح، بیایید آن را نادیده بگیریم. ما همچنین جنبه های مختلف پروتکل ضرب را برای اهداف نمایشی ساده کرده ایم.)

بینش در اینجا این است که ما می توانیم از cOT برای انجام ایمن این کار استفاده کنیم. در واقع، هر کدام ردیف آرایه مورب بالا را می توان دقیقاً با یک انتقال غافل همبسته مدیریت کرد. آلیس ورودی اصلی خود را وارد می کند i_A، به طور مناسب توسط j مراحل به سمت چپ؛ باب ورودی jᵗʰ بیت از ورودی اصلی او i_B. طبق تعریف coT، طرفین در نهایت به مدول سهم های افزودنی تصادفی می رسند q از یا 0 یا 2ʲ · i_A، بسته به بیت باب با انجام این کار برای هر ردیف به صورت جداگانه، طرفین به اشتراک گذاری افزودنی هر یک را به دست می آورند ردیف در بالا، در حالی که چیزی در مورد ورودی های یکدیگر در این فرآیند نمی آموزند. در نهایت، با اضافه کردن سهم های افزودنی محلی به دست آمده، طرفین دارای سهام افزودنی کل محصول می شوند. i_A · i_B. این دقیقا همان چیزی است که ما در بالا می خواستیم.

کار آینده. تکنیک های DKL قدرتمند و جالب هستند. این باعث می شود که تکنیک های آن برای درک، تعمیم و احتمالاً بهبود آسان تر شود. اشکال اصلی DKL ها نیاز به پهنای باند آن است که برابر با a است به طور نسبی بالا ~ 120 کیلوبایت (کل بایت های مبادله شده). تلاش برای کاهش این نیاز به پهنای باند، با بهبود تکنیک‌های DKLs جذاب خواهد بود. ما تلاش برای بهبود این پهنای باند را با استفاده از رویکردی شبیه Karatsuba در نظر گرفته‌ایم، اما هنوز موفق به جمع‌آوری جزئیات نشده‌ایم. تقریباً کاراتسوبا با تعویض هوشمندانه کار می کند یکی حاصل ضرب اعداد تمام قد توسط سه محصولات اعداد نیمه طول (و جابجایی این محصولات به صورت بازگشتی و غیره). نکته کلیدی که این رویکرد را سریعتر می کند این است که ضرب دو عدد نیمه طول فقط به a نیاز دارد ربع از کار به عنوان ضرب دو عدد تمام طول (به دلیل مقدار درجه دوم کار درگیر؛ به بالا مراجعه کنید). همه گفته شد، کاراتسوبا می تواند دو را ضرب کند nاعداد بیت در فقط

https://medium.com/media/4b4e72cc852ecf167dd90e8efa6f195e/href

عملیات اتمی، بر خلاف O(n2) با ضرب ساده مورد نیاز است. مشکل استفاده از این تکنیک برای DKL ها این است که خروجی های هر cOT باید مدول تصادفی باشد. q. این امر هر خروجی را مجبور می کند تا لاگ را بگیرد q بیت ها، زوج زمانی که اعداد واقعی درگیر در واقع به طور قابل توجهی کوچکتر از q. این مزایایی را که کاراتسوبا قرار است انتقال دهد بی اثر می کند – زیرا طول آن به نصف کاهش می یابد. دیگر نه به همین ترتیب پهنای باند را نصف می کند. این امکان وجود دارد که بتوان با استفاده از چند ایده جدید این کار را انجام داد.

اگر به رمزنگاری پیشرفته علاقه دارید، نقش های باز ما را اینجا بررسی کنید.

ECDSA سریع و ایمن 2-از-2 با استفاده از DKLs18 در ابتدا در The Coinbase Blog on Medium منتشر شد، جایی که مردم با برجسته کردن و پاسخ دادن به این داستان به گفتگو ادامه می دهند.

لینک منبع : هوشمند نیوز

آموزش مجازی مدیریت عالی حرفه ای کسب و کار Post DBA + مدرک معتبر قابل ترجمه رسمی با مهر دادگستری و وزارت امور خارجه	آموزش مجازی مدیریت عالی و حرفه ای کسب و کار DBA + مدرک معتبر قابل ترجمه رسمی با مهر دادگستری و وزارت امور خارجه	آموزش مجازی مدیریت کسب و کار MBA + مدرک معتبر قابل ترجمه رسمی با مهر دادگستری و وزارت امور خارجه
مدیریت حرفه ای کافی شاپ	حقوقدان خبره	سرآشپز حرفه ای
آموزش مجازی تعمیرات موبایل	آموزش مجازی ICDL مهارت های رایانه کار درجه یک و دو	آموزش مجازی کارشناس معاملات املاک_ مشاور املاک